О принципах практико-ориентированного обучения математике студентов технического университета

Введение

Современное развитие производства, социальные изменения и технологический прогресс требуют новых подходов к организации образовательного процесса в высшей школе. Выпускники высших учебных заведений должны осознавать свои профессиональные цели, быть способными принимать самостоятельные и компетентные решения, предполагающие саморазвитие и самореализацию в профессиональной деятельности.

Для образовательной подготовки выпускников инженерно-технических специальностей актуальной становится проблема усиления практико-ориентированного характера обучения. Решение этой задачи на уровне вуза возможно через внесение определенных изменений в учебный план и в учебные программы дисциплин подготовки будущих бакалавров. Структурирование и дополнение содержания обучения, внедрение и широкое применение новых форм и методов обучения (тренинги, практикум, групповая работа, проектные методы, проблемные задачи, ситуационные задачи, эвристические задачи и т.д.) с целью реализации практико-ориентированного обучения студентов математике требует определения соответствующих принципов организации образовательного процесса. Многие учёные-педагоги выделяют основные подходы, свойственные практико-ориентированному обучению:

• Создание условий для приобретения знаний, умений и опыта при изучении учебных дисциплин с целью формирования у студента мотивированности и осознанной необходимости приобретения профессиональной компетенции в процессе всего времени обучения в университете (Хозяинова, 2017, с. 158);
• Внедрение практико-ориентированных технологий обучения, способствующих формированию у студентов значимых для будущей профессиональной деятельности качеств личности, а также знаний, умений и навыков, обеспечивающих качественное выполнение профессиональных обязанностей по профилю подготовки (Хохлова, 2004, с. 19);
• Создание в университете новых форм профессиональной занятости студентов с целью решения ими реальных научно-практических и опытно-производственных работ в соответствии с профилем обучения (Хуторской, 2017, с. 85-91);
• Организация учебной, производственной и преддипломной практик студента с целью приобретения реальных профессиональных компетенций по профилю подготовки (Чудина, 2020, с. 235-239).

Выделенные подходы нельзя реализовать без приобретения студентами опыта деятельности, уровень которого определяется в логике компетентностного подхода. При этом компетентность следует понимать, как способность мобилизовать свои знания и опыт для решения конкретных задач по профилю будущей профессиональной деятельности.

Учебная дисциплина «Математика» играет решающую роль в учебной программе технического университета, поскольку обладает значительным потенциалом для образовательного и личностного роста. Математика является фундаментом формирования универсальных и базовых профессиональных компетенций; служит аналитическим инструментом, помогающим инженерам в решении проблем, организации и управлении различными аспектами производства, технологий и организации; позволяет инженерам критически мыслить в своей области и обеспечивает формальное и количественное описание реальных инженерных процессов. Следовательно, профессиональное образование будущих инженеров требует строгой математической подготовки. Выпускники технических университетов должны уметь в пределах своей специальности: строить математические модели; ставить математические задачи; выбирать подходящий математический метод и алгоритм для решения задач; применять для решения задач качественные математические и численные методы с использованием современных вычислительных машин; разрабатывать практические рекомендации на основе проведённого математического анализа.

Отечественные и зарубежные авторы указывают на различные подходы к определению основных принципов обучения студентов математике в техническом университете. Большинство ученых, говоря о принципах обучения в высшей школе, выделяют следующие: научности; фундаментальности и профессиональной направленности (Малыгина, 2008, с. 256); систематичности и последовательности (Hankeln et al., 2019); активности и сознательности (Васильева, 2014, с. 23); принцип связи теории с практикой и обучения с жизнью (Бровка, 2014, с. 98); проблемности, наглядности, доступности, целенаправленности (Bergsten et al., 2015); направленности обучения на решение во взаимосвязи задач образования, воспитания и развития (Dreher et al., 2019); единства конкретного и абстрактного в обучении (Magana et al., 2017); деятельностного содержания (2018, с. 28–36). Данные принципы реализуются как в учебном процессе в целом, так и в отдельных его компонентах. Согласно принципу первичности практико-ориентированной учебной деятельности, предлагаемым Е.Г. Евсеевой, студент должен осознавать практико-ориентированный результат своей учебной деятельности, и какие учебные действия привели к этому результату. Мы разделяем позицию Е. Г. Евсеевой, что в ходе решения практико-ориентированных задач следует целенаправленно формировать понимание того, в какой области профессиональной деятельности будут востребованы приобретаемые математические умения и навыки (2018, c. 28–36).

Методы и методология

Проблеме практико-ориентированного обучения уделяется значительное место в методических исследованиях. Так, например, Ю.А. Кустов в работе (1990, c. 18) подчеркивает, что практико-ориентированная направленность, являющаяся ведущим принципом, отражающим конечную цель педагогического процесса в высших учебных заведениях, диктует следующие единые для всех звеньев образования требования к системе преемственности: специальность должна быть тем каркасом, на котором строится вся разносторонняя подготовка квалифицированных специалистов; подготовка в технических вузах должна вестись непрерывно и одновременно в тесном взаимодействии с общетеоретическими и общетехническими дисциплинами.

Исследуя психологические аспекты проблемы практико-ориентированного обучения в вузе, М. И. Дьяченко и Л. А. Кандыбович, приходят к следующему выводу: «Формировать практико-ориентированную направленность у студентов – это значит укреплять у них положительное отношение к будущей профессии, интерес, склонности и способности к ней, стремление совершенствовать свою квалификацию после окончания вуза, развить идеалы, взгляды, убеждения, престиж профессии в собственных глазах будущего специалиста» (1981, c. 73).

Cогласно требованиям современного образовательного стандарта по специальности «Информационные системы и технологии в проектировании и производстве», в процессе математической подготовки студенты технического университета должны овладеть следующими универсальными компетенциями (УК) (ОСВО, 2023): быть способным к саморазвитию и совершенствованию в профессиональной деятельности (УК-5); решать стандартные задачи профессиональной деятельности на основе применения информационно-коммуникационных технологий (УК-2); обладать навыками творческого аналитического мышления (УК-11). К базовым профессиональным компетенциям (БПК), формируемым в процессе изучения дисциплин «Теория вероятности и математическая статистика», «Специальные математические методы и функции» отнесены компетенции (ОСВО, 2023): взаимодействовать со специалистами смежных профилей (БПК-22); анализировать и оценивать собранные данные (БПК-23); разрабатывать бизнес-планы создания новых информационных технологий (БПК-27); оценивать конкурентоспособность и экономическую эффективность разрабатываемых информационных технологий (БПК-28).

Под практико-ориентированным обучением математике в техническом университете будем понимать обучение, предусматривающее целенаправленную реализацию сопутствующих и перспективных содержательных межпредметных связей математики и профессионально-ориентированных дисциплин как необходимого условия формирования основ базовых профессиональных и универсальных компетенций студентов технического вуза. Выбор принципов практико-ориентированного обучения математике студентов технических специальностей, по нашему мнению, определяется методологическими подходами, на основе которых проектируется обучение. Методологическими основаниями практико-ориентированного обучения математике студентов инженерно-технических специальностей являются: личностно-ориентированный, компетентностный, деятельностный, контекстный, системный подходы.

Предложенные Е. Г. Евсеевой, согласно парадигме деятельностного подхода к обучению, принципы практико-ориентированной математической подготовки студентов технических специальностей, нами дополнены принципом актуализации универсальных компетенций, первичности практико-ориентированной учебной деятельности, принципом практико-ориентированного целеполагания и определения содержания обучения, принципом межпредметной интеграции, принципом активного включения.

Принцип актуализации универсальных компетенций предполагает, что, формируя содержание учебной программы по математике, следует руководствоваться, прежде всего, квалификационными требованиями образовательного стандарта. В результате освоения образовательной программы у будущих инженеров-программистов должны быть сформированы, в частности, компетенции, имеющие практико-ориентированный характер: навыки анализа исходных и выходных данных решаемых задач и формами их представления; умения выполнять алгоритмизацию инженерных задач, проводить анализ предметной области и формировать логическую и физическую структуру соответствующей базы данных, оценивать эффективность алгоритмов взаимодействия с БД, разрабатывать модели оценки надежности для конкретных программных продуктов на основе положений действующего образовательного стандарта. В процессе овладения математическими знаниями, в ходе построения и решения математических моделей у студентов должны быть развиты способности: к абстрактному мышлению, анализу, синтезу; решать задачи профессиональной деятельности на основе информационной и библиографической культуры с применением информационно-коммуникационных технологий и с учетом основных требований информационной безопасности; проводить эксперименты по заданным методикам с обработкой и анализом результатов.

Согласно принципу первичности практико-ориентированной учебной деятельности студент должен осознавать практико-ориентированный результат своей учебной деятельности, и какие учебные действия привели к этому результату. В ходе решения практико-ориентированных задач следует целенаправленно формировать понимание того, в какой области профессиональной деятельности будут востребованы приобретаемые математические умения и навыки. Так, например, освоение машинного обучения и искусственного интеллекта невозможно без знаний математического анализа и дифференциальных уравнений. Модели машинного обучения часто оптимизируют с помощью градиентного спуска. Цель такой оптимизации – найти набор параметров модели, которые минимизируют определенную функцию потерь. В алгоритме обратного распространения, который используется для обучения нейронных сетей, градиенты функции потерь относительно весов и смещений сети вычисляются с помощью цепного правила. Многие задачи в машинном обучении и искусственного интеллекта связаны с решением дифференциальных уравнений, которые описывают скорость изменения системы во времени. Решение этих уравнений позволяет моделировать широкий спектр физических и биологических систем – от распространения болезней до поведения финансовых рынков.

Принцип практико-ориентированного целеполагания и определения содержания обучения заключается в создании условий, при которых будут формулироваться и осознаваться студентами цели обучения математике в процессе практико-ориентированных учебных действий. Студенты при изучении каждой конкретной темы математической дисциплины, исходя из этого, ставят цель и формулируют задачи для освоения темы, выбирают форму и темп обучения. Эффективность реализации данного принципа в обучении студентов технических специальностей существенно зависит от структурирования содержания обучения математике, выбора методов обучения. Важно, также, умение преподавателя помочь студенту осознать практическую значимость учебного материала каждого занятия по математике в профессиональной деятельности инженера. Соблюдение этого принципа ориентирует на конструирование практико-ориентированного результата учебной деятельности студентов. Следует развивать у них умение самостоятельно формулировать цели изучения каждой темы математической дисциплины, выделять в ней микроцели. Найденные студентом способы достижения цели, осознание практической значимости изучения конкретных разделов математики, предложенные методы осуществления этих способов, являются продуктами их образовательной деятельности.

Принцип межпредметной интеграции заключается в определении содержательных и методологических связей математики с дисциплинами естественно-научного цикла подготовки, а также в использовании материала этих дисциплин при изучении математики. Применение данного принципа в процессе обучения математическим дисциплинам позволяет устранить существующее противоречие между преимущественно теоретическим характером изучения математического содержания дисциплин и необходимостью практического навыка применения теоретических знаний в профессиональной деятельности. Рассмотрим реализацию этого принципа на примере решения следующей задачи:

Задача. Материальный ущерб, принесённый предприятию «Смартмашин» в ходе сертификации оборудования, изменяется в зависимости от величины  по формуле:

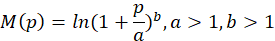 – некоторые постоянные, 0 ⩽, p ⩽, 0,2,

где p – количество неисправных машин на предприятии (дес. шт.).

Аппроксимировать функцию M(p) линейной функцией и оценить погрешность оценки.

С позиций математики задача сводится к разложению функции в ряд Маклорена и оценке погрешности вычислений:

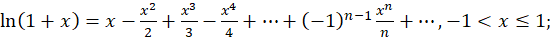  (1)

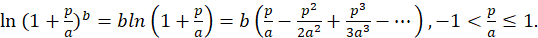   (2)

Поскольку по условию задачи функцию M(p) необходимо аппроксимировать линейной функцией, то в разложении (2) нужно взять только первый член ряда: 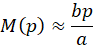. При этом допущенная погрешность не превосходит первого отброшенного члена ряда, т.е. 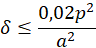. Наибольшая погрешность в вычислениях будет допущена при максимальном значении параметра p:p = 2 и, соответственно, .

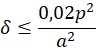С позиций профессиональной подготовки специалиста решение задачи способствует формированию у студентов умений: анализировать рабочую обстановку по таким параметрам, как количество неисправного оборудования и размер материального ущерба, понесённого во время сертификации; определять зависимость размера ущерба от количества сломанного оборудования; выполнять прогноз о размере ожидаемого ущерба; оценивать точность сделанного прогноза. При соблюдении принципа межпредметной интеграции студент получает возможность изучения фундаментальных понятий математики в предметном поле будущей профессиональной деятельности, естественнонаучных и специальных дисциплин.

Принцип активного включения реализуется в образовательной практике с помощью эвристического обучения. Приведём примеры эвристических заданий по дисциплине «Дискретная математика», предлагаемых студентам первого курса факультета информационных технологий и робототехники Белорусского национального технического университета специальности 6-05-0611-01 «Информационные системы и технологии в проектировании и производстве», которые способствуют активизации самостоятельной деятельности, включённости в процесс коммуникации и осмыслению понятий математики.

А. Эвристическое задание по теме «Бинарные отношения в бизнес-процессах»:

Преамбула задания: В математике бинарное отношение можно рассматривать как расширение понятия функции, т.е. бинарным отношением между множествами А и В называется любое подмножество Р декартова произведения множества А на множество В. Часто, чтобы обозначить принадлежность упорядоченной пары (a, b) к бинарному отношению Р используют обозначения Р(a, b) или aР. При этом говорят, что  находится в отношении Р к. В бизнес-процессе задание направляется не одному исполнителю, а множеству возможных исполнителей. Выполняет это задание тот пользователь, который первым возьмет его на исполнение. Для автоматизации процессного управления предприятиями разработан специальный класс компьютерных систем – системы управления бизнес-процессами и административными регламентами (далее СУБПиАР).

Постановка задания:

1. Приведите от трёх до пяти примеров возможностей инициализации ролей при помощи функций над исполнителями с применением бинарных отношений. Возможность использования отношений для инициализации ролей бизнес-процессов реализуйте в промышленной СУБПиАР.
2. Зададим отношение в СУБПиАР как множество пар (Исполнитель 1, Исполнитель 2), в которых Исполнитель является пользователем или группой пользователей. Опишите алгоритм инициализации роли в этом случае.
3. Создайте концепцию отношений в интерфейсе среды исполнения бизнес-процессов.

В. Эвристическое задание по теме «Моделирование логистических процессов на предприятии с помощью графов»

Преамбула задания: Сфера анализа процесса закупок на производственном предприятии обширна. Анализ процесса закупок можно разделить на две группы: анализ протекания процессов закупок и управленческий анализ процессов закупок.

Постановка задания:

1. Приведите три-четыре примера использования графов на экономическом (логистическом) предприятии на примере поставок, транспортных закупок, логистических затрат.
2. Представьте иерархию управленческого анализа логистических процессов конкретного предприятия с помощью графа. Дерево графа может быть нисходящим и изображать следующие методы экономического анализа: динамические сравнения, сравнения с эталоном, пространственные сравнения и др.
3. Постройте граф, отображающий анализ процесса закупок с описанием соответствующих характеристик и критериев: анализ объёма, динамики и структуры закупок, анализ складских процессов, эффективность складских инвестиций, выбор источников закупок и др.

Указание: Граф, а также иерархию управленческого анализа можно построить в конструкторе диаграмм draw.io, используя ссылку https://app.diagrams.net.

По мнению авторов, на практико-ориентированное обучение математике в техническом университете существуют два взгляда. Во-первых, под ним понимается система потребностей, мотивов, интересов и склонностей, выражающих отношение личности к будущей профессии. Систематическое ознакомление студентов с их общей профессиональной деятельностью и встречи с лучшими представителями выбранной специальности интенсифицируют процесс формирования практико-ориентированного обучения. Другой взгляд на практико-ориентированное обучение в техническом вузе состоит в том, что рассматривается содержание образования, проблемы его построения: имеются существенные различия между принципом практико-ориентированной направленности и общим принципом связи теории с практикой. Реализация первого принципа не противоречит второму, однако принцип практико-ориентированной направленности предусматривает не только связь с производственным обучением, он требует включать и теоретическое обучение, а также организацию межпредметных связей специальных дисциплин, использование практико-ориентированного обучения в учебном процессе по общеобразовательным предметам.

Результаты и их обсуждение

Практико-ориентированная направленность обучения математике в вузе имеет сложную структуру, не сводимую только к формированию универсальных компетенций или к воспитательным мероприятиям. Наряду с мотивационно-целевыми аспектами, она непосредственно касается существа вопросов отбора содержания образования, форм и методов обучения. Решение этих вопросов является важнейшим дидактическим условием успешной организации практико-ориентированного обучения математике. Курс математики в технических вузах должен отвечать требованиям фундаментальности и профессиональной направленности, которые не противоречат друг другу, а способствуют общей образованности студентов и их профессиональной подготовке. Реализация в обучении математике принципов практико-ориентированного обучения предполагает развитие мышления и формирование универсальных и базовых профессиональных компетенций; обеспечение математического аппарата для изучения специальных дисциплин и профессиональной подготовки; формирование навыков непрерывного самообразования и развития. Перечисленные задачи требуют решения на содержательном и методическом уровнях организации процесса обучения с учетом специфики математики как науки и как учебного предмета.

Заключение

Считая хорошую математическую подготовку неотъемлемой частью полноценного инженерного образования, Б.В. Гнеденко обращает внимание на то, что «математическое образование – это не только передача сведений по различным областям математики, знакомство с ее результатами, понятиями и методами исследования, но и формирование научного мировоззрения» (1981, с. 45). Поэтому учить математике, как утверждает Б.В. Гнеденко, «следует не вообще, а так, чтобы содействовать познанию закономерностей окружающего мира; чтобы обучающиеся ясно представляли себе происхождение основных понятий и процесс научного прогресса; чтобы студенты одновременно получали навыки практического использования теории, которые являлись бы естественным условием развития теоретического знания; учить так, чтобы полученные знания не были бесполезным грузом, а постоянно использовались на практике» (1981, с. 63).

В результате анкетирования студентов 1-ых и 4-ых курсов Белорусского национального технического университета факультета информационных технологий и робототехники (82,4 % опрошенных составили первокурсники (80 человек) и 94,7 % – выпускники (90 человек)) было установлено, что в качестве ведущего мотива практико-ориентированного обучения признана возможность, во-первых, получить серьёзную, фундаментальную математическую подготовку, во-вторых, освоить методы современных компьютерных разработок. Таким образом, практико-ориентированная математическая подготовка становится всё более значимой по мере того, как выступает основанием для систематизации и решения практико-ориентированных, прикладных задач.

Принципы практико-ориентированного обучения математике студентов технического университета регулируют в образовательном процессе соотношение общего и специфического, определяют диалектику взаимодействия целостного развития личности и ее особенного, профессионального. Именно это обстоятельство предопределяет особую дидактическую значимость этих принципов в современном образовании будущих инженеров.

Бровка, Н. В. (2014). О реализации компетентностного подхода в обучении студентов математике. Веснік Брэсцкага універсітэта. Серыя 3. Філалогія. Педагогіка. Псіхалогія, 2, 98–104.

Васильева, М. А. (2014). Профессионально-прикладная направленность обучения математике как средство формирования математической компетентности: на примере аграрного вуза. PhD Thesis, Саранск.

Гнеденко, Б. В. (1981). Математическое образование в вузах. Москва.

Дьяченко, М. И. & Кандыбович, Л. А. (1981). Психология высшей школы. Минск: Высш. школа.

Евсеева, Е. Г. & Попова, С. С. (2018). Математическое моделирование в профессионально ориентированном обучении математике будущих химиков. Международный сборник научных работ «Дидактика математики: проблемы и исследования», Вып. 48, 28–36.

Кустов, Ю. А. (1990). Творческие основы преемственности профессиональной подготовки молодёжи в профессионально-технических училищах и технических вузах. PhD Thesis, Казань.

Малыгина, О. А. (2008). Обучение высшей математике на основе системно-деятельностного подхода: учеб. пособие. Москва: Изд-во ЛКИ.

Образовательный стандарт высшего образования (ОСВО 6-05-0611-01-2023) (2023). Минск: Министерство образования Республики Беларусь.

Хозяинова, М. С. (2017). Обучение содержательному анализу математического материала при изучении алгебры в техническом вузе. PhD Thesis, Сыктывкар.

Хохлова, М. В. (2004). Методика конструирования системы задач и ее применение в обучении математике студентов технических ВУЗов. PhD Thesis, Киров.

Хуторской, А. В. (2017). Методологические основания применения компетентностного подход к проектированию образования. Высшее образование в России, 12, 85–91.

Чудина, Е. Ю. (2020). Реализация принципа внутренней дифференциации при обучении математике в условиях дистанционного обучения в инженерном вузе. Вестник Донецкого национального университета. Серия Б. Гуманитарные науки, 3, 235–239.

Bergsten, C., Engelbrecht, J. & Kågesten O. (2015). Conceptual or procedural mathematics forengineering students – views of two qualified engineers from two countries. International Journal of Mathematical Education in Science and Technology, 46 (7), 979–990. (In English)

Dreher, R., Gornov, A., & Kondratyev, V. (2019). Concept of the Natural Structure of Engineering Training and the Code of Professional Ethics of an Engineer. Higher Education in Russia, 28 (1), 76–85. (In English)

Magana A. J., & Coutinho, G. S. (2017). Modeling and simulation practices for a computational thinking-enabled engineering workforce. Comput. Appl. Eng. Educ, 25 (1), 62–78. (In English)

Hankeln, C., Adamek, C. & Greefrath G. (2019). Assessing Sub-competencies of Mathematical Modelling Development of a New Test Instrument. Lines of inquiry in mathematical modelling research in education, 143–160. (In English)