О теоретических основаниях использования наглядного моделирования при обучении учащихся курсу алгебры
На основании проведенного анализа понятий «наглядность», «наглядное обучение», «модель» в статье дается определение специфики использования метода наглядного моделирования при обучении учащихся математике в средних общеобразовательных учреждениях. Делается акцент на отсутствие исследований вопроса использования метода наглядного моделирования при обучении учащихся алгебре. Обращается внимание на недопустимость чрезмерного использования наглядности на уроках математики, так как это приводит к нарушениям в развитии воображения, наблюдательности и пространственного мышления.
Новому этапу развития общества соответствуют новые задачи образования, реализация которых выдвигает новые требования к организации учебно-воспитательного процесса с учащимися в средних общеобразовательных школах. В настоящее время основной целью функционирования современной общеобразовательной школы является создание условий для обеспечения качественного образования личности, способной к интеграции знаний, к самообучению и самореализации в современном обществе, к освоению инноваций в системе обучения. Традиционно, востребованы такие формы обучения, которые бы обеспечили развитие мотивационной сферы учащихся, умений осуществлять самоуправление учебно-познавательной деятельностью, обеспечивали более глубокое усвоение содержания курса математики, в частности в 10 – 11 классах. На пути инновационного развития потенциала общего среднего образования в условиях информационного общества в наше время обучение математике в средней школе пересматривается. Эта реформа направлена на раскрытие социального статуса математики, обоснование структуры ее внутренних и внешних взаимосвязей, актуализирующих при этом интегральные конструкты отдельных разделов и тем как дидактических единиц. Большое значение в этой связи придается большей визуализации и использованию наглядного моделирования.
Одним из методов, способствующих глубокому, наглядному и осознанному усвоению алгебраического содержания курса математики является активное использование наглядного моделирования на уроках.
Вопросами наглядности и моделирования в области геометрии содержания школьного курса математики занимались Я. И. Груденов, Г. И. Глейзер, Ю. М. Колягин, Н. М. Рогановский, И. Ф. Шарыгин, В. В. Шлыков. Отдельно вопрос использования метода наглядного моделирования при обучении учащихся алгебре в научно-методических исследованиях не рассматривался.
Наглядность алгебраического образа, возникающего у учащегося, зависит главным образом от уровня развития познавательных способностей, от самого учащегося, от его интересов, наконец от его потребности, желания создать для себя яркий, понятный образ этого объекта, усвоить приобретаемые знания.
Для эффективного усвоения математических знаний алгебраического курса одной наглядности недостаточно – к ней нужно присоединить активную деятельность самого учащегося. Данная деятельность заключается в процессе создания модели – моделировании.
Моделирование способствует формированию диалектико-материалистического мировоззрения. Введение в содержание обучения понятий модели и моделирования существенно меняет отношение учащихся к учебному предмету, делает учебную деятельность более осмысленной и продуктивной. При этом важно, чтобы учащиеся сами овладели методом моделирования, научились строить модели и изучать уже готовые модели, отражая различные отношения и закономерности алгебраических объектов. В учебной программе по учебному предмету «Математика» в 10 – 11 классах не предусмотрено рассмотрение понятия модели, однако, его использование учащимися может быть очень продуктивно.
Существенные признаки алгебраических объектов и их связи, зафиксированные в модели, становятся наглядными для учащихся тогда, когда эти признаки, связи были выделены самими учащимися в их собственной учебной деятельности, т.е. тогда когда они сами участвуют в создании модели. В противном случае учащиеся не видят их в модели, и она теряет наглядность. Построение модели учащимися обеспечивает наглядность существенных свойств, скрытых связей и отношений, все остальные свойства, несущественные в данном случае, отбрасываются. Наглядность позволяет учащимся наблюдать конкретные алгебраические объекты. Однако не все учащиеся и не сразу умеют обнаружить основные специфические свойства рассматриваемого объекта, выявить их различия и сходства. В наибольшей мере этому способствует моделирование, так как модель включает единство общего и частного, логического и чувственного в изучаемых объектах.
Для учащихся при изучении математики структура изучаемых математических объектов и их существенные связи не всегда выступают за знаками, выраженными в буквенно-цифровой и графической форме.
Следует отметить, что моделирование и наглядность имеют общую цель – выделение главного, существенного в изучаемых объектах и предметах, но только при использовании наглядности существенное выделяется в виде восприятия, а при моделировании – в действии, преобразующем объект [1].
Для указанной выше цели учителю необходимо с учащимся рассматривать наглядность в целостном процессе обучения математике в тесной связи со знаково-символической деятельностью в направлении оптимального учета психологических закономерностей восприятия, мышления, воображения и памяти. Задача учителя научить видению закономерностей и зависимостей в разнообразии и сходстве алгебраических объектов, выраженных в буквенно-цифровой и графической форме.
В настоящее время в методической и психолого-педагогической литературе наблюдается разнообразие подходов к определению понятия «наглядность».
В связи с многозначностью термина «наглядность» рассмотрим различные его определения.
Ян Амос Коменский, Иоганн Фридрих Гербарт, Фридрих Адольф Вильгельм Дистервег, Иоганн Генрих Песталоцци, Фридрих Вильгельм Август Фрёбель, Николай Фёдорович Бунаков, считали, что наглядное обучение имеет непосредственную связь с конкретно воспринимаемыми объектами и явлениями, действующими на органы чувств. Педагоги-ученые того времени поставили впервые проблему наглядного обучения, обосновали значение наглядного обучения, а также добились весомых успехов в разработке методики его применения в школе, поставили вопрос о связи деятельности учащихся с наглядным обучением. Они считали, что наглядность присуща только конкретному объекту, а абстрактному нет. Такого мнения придерживались ученые педагоги того времени, и всячески отказывались от связи абстрактного с понятием наглядности.
Согласно психологу З. И. Калмыковой, под высшей формой наглядности понимается практическое действие с предметом. Практическая форма наглядности связана, по ее мнению, не только с натуральными объектами, действиями с ними (природными, бытовыми, производственными объектами), но и предполагает выполнение действий учащимися с предметами, их заменяющими (чертежами, схемами, графиками, рисунками). К практической форме наглядности относятся действия с этими средствами наглядности, доступные наблюдению, а также мыслительный эксперимент.
По мнению С. Л. Рубинштейна, принцип наглядности вытекает из сущности процесса восприятия, осмысления и обобщения обучаемыми изученного материала. Мыслить человек начинает тогда, когда у него появляется потребность что-то понять. Мышление всегда начинается с проблемы или вопроса, с удивления или недоумения. Этой проблемной ситуацией определяется вовлечение личности в мыслительный процесс: он всегда направлен на решение какой-либо задачи.
Таким образом в конце XX века ученые-педагоги в своих работах в большей степени наглядное обучение связывали с конкретно воспринимаемыми объектами или явлениями, которые действовали на органы чувств и активизировали деятельность учащихся. Заслуга ученых-педагогов того времени состоит в том, что они: остро поставили вопрос наглядного обучения; дали обоснование наглядного обучения (К. Д. Ушинский); впервые занялись разработкой методики применения его в школе; стали впервые рассматривать вопрос о связи деятельности с наглядным обучением.
Исторический подход к наглядности в обучении математике как к опоре на чувственное восприятие дает максимальный эффект в начальной школе при обучении учащихся математике и явно недостаточен при изучении высших разделов математики.
В связи с этим следует рассмотреть понятие наглядности в работах современных исследователей в области психологии, педагогики и методики преподавания математики.
С точки зрения психологов Н. А. Менчинской, П. Я. Гальперина, Т. В. Кудрявцева, Л. В. Занкова, Л. Л. Гуровой, В. С. Мухиной, А. Н. Леонтьева и в нашем понимании, наглядность понимается как восприятие учебного материала на абстрактном уровне и в процессе практической деятельности, которая включает в себя процесс восприятия, осмысления и обучение изученному материалу.
Существуют различные подходы к определению понятия наглядности, которые объединены идеей о том, что наглядность – это целенаправленный познавательный процесс, в результате которого при взаимодействии субъекта со знаковыми системами в его сознании генерируются наглядные образы. Таким образом, формируется визуальное представление излагаемого материала.
Согласно педагогу исследователю Л.Н. Нуридиновой, понятие наглядности связано с понятием образа, который бывает двух видов. В первую группу входят образы чувственно-наглядные, отражающие непосредственно реальные объекты. Ко второй группе, рациональные образы, отражающие в абстрактной форме наиболее общие, существенные связи и стороны объективного мира, недоступные непосредственному чувственному восприятию.
Педагоги М. Я. Демьяненко и К. А. Лазаренко, С. Ф. Мельник, А. П. Ланг, понимают наглядность как целенаправленный и специально организованный показ учебного материала, который подсказывает учащимся законы либо закономерности изучаемого явления, а также позволяет открыть законы и убедиться в их достоверности.
Мы разделяем с педагогом Э. Г. Мингазовым [3] определение понятия наглядности и считаем целесообразным рассматривать его на двух ступенях: конкретной и абстрактной (на уровне взаимодействия субъекта со знаковыми системами), так как учащийся должен иметь четкое визуальное представление излагаемого материала и так же уметь взаимодействовать с субъектом на уровне знаковых систем.
Рассмотрим трактовку понятия наглядности с точки зрения математиков и методистов в области методики преподавания математике.
Согласно советскому математику В. Г. Болтянскому, наглядность – изоморфизм и простота. «…для обсуждения вопроса о наглядности необходимо иметь две модели явления: первая из них – это абстрактная модель, т.е. теория явлений, которую мы должны сформировать в сознании учащегося, и вторая – вспомогательная, учебная модель. О наглядности имеет смысл говорить только в применении ко второй модели, если она изоморфна первой модели и обладает простотой восприятия».
А. А. Столяр, Р. С. Черкасов считают, что наглядность в обучении математике особенно важна, так как здесь требуется достижение более высокой степени абстракции, чем в обучении другим предметам, а она содействует развитию абстрактному мышлению. Из различных видов наглядности широкое применение, по мнению методистов, в обучении математике находит символическая наглядность, к которым относят: чертежи, графики, схемы, таблицы. Под средствами символической наглядности понимали условную знаковую систему, с помощью которой изучаемая сторона предметов, явлений, процессов отделялась от прочих свойств и представлялась в чистом виде.
Н. М. Рогановский писал, что наиболее общей характеристикой наглядности является модельное представление знаний. При этом для построения модели используются более наглядные теории. В результате наглядность абстрактной теории усиливается при помощи абстрактного, более наглядного знания, однако в своих исследованиях автор занимается моделированием при обучении геометрии.
С. А. Гастеев, Б. И. Крельштейн, С. Е. Ляпин, М. М. Шидловская считали, что осуществление принципа наглядности при изучении математики состоит в наблюдении различных предметов, моделей, чертежей, рисунков, а также в использовании опыта и представлений, накопленных учащимися. Придерживались мнения, что толкование арифметических и алгебраических фактов весьма ценно через геометрические построения.
Многие ученые дают определение наглядности как принципа, способствующего в процессе обучения учащихся более эффективность восприятию, осмыслению и обобщению ими изучаемого материала, а также опыта и представлений, накопленных учащимися при познании объектов окружающего мира.
К концу XX в. понятие наглядности в обучении изменилось по сравнению с первоначальными данным в 30-40-ых годах XX в. В настоящее время оно рассматривается как на конкретном, так и на абстрактном уровне, и в процессе деятельности.
Для эффективного усвоения знаний одной наглядности недостаточно – к ней нужно присоединить активную деятельность самого учащегося. Данная деятельность заключается в процессе создания модели – моделировании.
Многие исследователи занимались проблемой изучения понятия «модели».
Модель как систему, рассматривал А. И. Уемов, исследование которой служит средством для получения информации о другой системе.
Под моделью Н. В. Кузьмин понимал искусственное создание для изучения явления (предмет, процесс, ситуация и т.д.), исследование которого затруднено или вовсе невозможно.
Мы считаем наиболее ярким и отличающимся простотой понимания сущности понятия модели определение данное В. А. Штоффом. Он определил модель как мысленно представляемую или материально реализованную систему, которая, отражая или воспроизводя объект исследования, способна замещать его так, что изучение ее дает нам новую информацию об этом объекте. Эта же мысль подчеркивалась в исследованиях Н. Г. Салминой и Л. М. Фридманом.
Согласно С. А. Бешенкову, модель – это искусственно созданный объект в виде схемы, физических конструкций, знаковых форм или формул, который, будучи подобен исследуемому объекту (или явлению), отображает и воспроизводит в более простом и огрубленном виде структуру, свойства, взаимосвязи и отношения между элементами этого объекта.
На основании анализа определений «модели» мы выбираем вариант, предложенный в работах В. А. Штоффа, Л. М. Фридмана и В. В. Давыдова: «Модель» – система свойств и закономерностей, описывающих данный объект, способствующая получению знаний о другом объекте-оригинале или прототипе модели, дающая новую информацию об объекте.
Определены следующие свойства модели:
- Модель – средство познания.
- Модель представитель оригинала, который в каком-либо отношении более удобен для изучения и может при этом перенести полученные знания на сам объект.
- Модель характеризуется существенными свойствами прототипа.
- Модель однозначно соответствует оригиналу.
Существенные признаки и связи, зафиксированные в модели, становятся наглядными для учащихся тогда, когда эти признаки, связи были выделены самими учащимися в их собственной учебной деятельности, т.е. тогда когда они сами участвовали в создании модели. В противном случае учащиеся не видят их в модели, и она теряет наглядность. Построение модели учащимися обеспечивает наглядность существенных свойств, скрытых связей и отношений, все остальные свойства, несущественные в данном случае, отбрасываются.
Таким образом для указанной выше цели учащимся необходимо рассматривать наглядность в целостном процессе обучения математике в тесной связи со знаково-символической деятельностью в направлении оптимального учета психологических закономерностей восприятия, мышления и памяти.
Идея наглядного моделирования разработана Е. И. Смирновым, её придерживаются такие российские ученые как В. С. Абатурова, В. Л. Жолудева, Н. Д. Кучугурова, И. Н. Мурина, В. Н. Осташков, Т. В. Скоробогатова, Е. Н. Трофимец, В. В. Богун. Все исследования названных авторов касаются вузовского обучения студентов. В Республике Беларусь в последнее десятилетие диссертационных исследований? посвященных использованию наглядного моделирования в средней школе нами не обнаружено.
Наглядное моделирование определяется Е. И. Смирновым [5] как процесс формирования адекватного категории диагностично поставленной цели устойчивого результата внутренних действий обучаемого на основе моделирования существенных свойств, отношений, связей и взаимодействий при непосредственном восприятии приемов знаково-символической деятельности с отдельным математическим знанием или упорядоченным набором знаний.
Разделяя точку зрения Е. И. Смирнова на понятие наглядного моделирования мы считаем, что данное определение очень обобщено. Нам кажется целесообразным акцентировать внимание в определении на специфике наглядного моделирования при обучении математике учащихся средних школ.
Специфика наглядного моделирования в обучении математике состоит в возможности формирования осознанного распознавания и восприятия учащимися структуры модели, свойств, закономерностей, отношений, взаимосвязей её составляющих частей, что способствует в большей мере устойчивому запоминанию, развитию мышления и воображения при познании объектов окружающего мира.
Таким образом данный подход к наглядному моделированию состоит в формировании осознанного распознавания и восприятия модели, для самостоятельного выделения учащимися свойств, закономерностей, взаимосвязей, которые необходимы для изучения моделей и соответствуют оригиналу изучаемого объекта.
Учителю необходимо помнить о том, что чрезмерное использование наглядности в обучении учащихся мешает развитию воображения, наблюдательности и пространственных представлений. Целесообразно помнить о необходимости умеренного использования наглядности. В методике преподавания алгебры целесообразно использовать дифференцированный подход к обучению учащихся с целью использования метода наглядности в различных группах учащихся с различной частотой (по усмотрению учителя).
Рассмотрим примеры использования наглядного моделирования при обучении учащихся курсу алгебры.
|
Пример 1. Найдите значение выражения: |
||
|
Вид наглядного моделирования: визуализация процесса нахождения алгебраического выражения |
||
|
Решение |
||
|
Шаг |
Формульная запись |
Наглядная модель |
|
1 |
Пусть |
|
|
2 |
Пусть |
|
|
Таким образом, задание сводится к нахождению значения выражения вида ctg(α+β). |
||
|
Рассмотрим ΔABC, по т. Пифагора CB=4x. |
||
|
Рассмотрим ΔADM, по т. Пифагора |
||
|
3 |
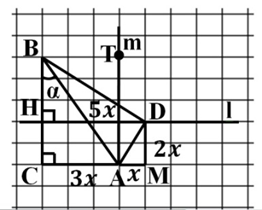
Из вершины D прямоугольного треугольника ΔADM проведем прямую l,l⊥CB,l∩CB=H. Соединим вершины треугольников B и D. Проведем прямую m,A∈m,m||CB,m||MD |
|
|
α+β=∠BAD, так как ∠CBA=∠BAT=α, как внутренние накрест лежащие при пересечении CB||m, секущей BA, а также ∠MDA=∠TAD=β, как внутренние накрест лежащие при пересечении DM||m, секущей AD. Следовательно, найдем значение ctg∠BAD. |
||
|
Рассмотрим ΔBHD, по т. Пифагора |
||
|
Рассмотрев ΔBAD и применив теорему косинусов, получаем cos(α+β)=55, тогда sinα+β=255, значит ctg(α+β)=55⋅525=12. |
||
|
Ответ: 1/2. |
||
Таким образом, использование метода наглядного моделирования при обучении учащихся математике должно включать в себя процесс проектирования и построения модели, а также формирование адекватного результата внутренних действий, выражающихся в учебной деятельности. «Наглядная модель» должна рассматриваться как устойчивая ассоциация, как простые геометрические формы, как психологические основы осознанности усвоения знаний.
- Ушинский К.Д. Собр. соч. : в 12 т. Москва: АПН РСФСР, 1948. Т. 11. С. 52-53.
- Фридман Л.М. Наглядность и моделирование в обучении. Москва: Знание, 1984. 80 с.
- Мингазов Э.Г. Гносеологические основы принципа наглядности в обучении // Сов. педагогика, 1975, № 9, С. 13–18.
- Штофф В.А. Моделирование и философия. Москва: «Наука», 1966. 301 с.
- Смирнов Е.И. Наглядное моделирование в обучении математике: теория и практика: Учебное пособие. Ярославль: Изд-во ЯГПУ, 2007. 454 с.
- Давыдов В.В. Психологическая теория учебной деятельности и методов начального обучения, основанных на содержательном обобщении. Томск: Пеленег, 1992. 283 с.
- Рубинштейн С.Л. Проблемы общей психологии. М.: Педагогика, 1973. 416 с.
- Колягин Ю.М. и др. Методика преподавания математики в средней школе. Общая методика. Учеб. пособие для студентов физ.-мат. факультетов пед. вузов. М.: Просвещение, 1975. 462 с.
- Рогановский Н.М., Рогановская Е.Н. Методика преподавания математики в средней школе. Часть 1: Общие основы методики преподавания математики (общая методика) Могилев: МГУ им. А.Л. Кулешова, 2010. 312 с.
- Черкасов Р.С., Столяр А.А. Методика преподавания математики в средней школе. М.: Просвещение, 1985. 336 с.


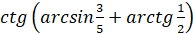 .
.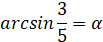 , тогда
, тогда 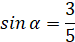 . Построим прямоугольный треугольник с углом α, так чтобы
. Построим прямоугольный треугольник с углом α, так чтобы 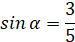 , т.е. противолежащий катет к α и гипотенуза пропорциональны числам 3 и 5.
, т.е. противолежащий катет к α и гипотенуза пропорциональны числам 3 и 5.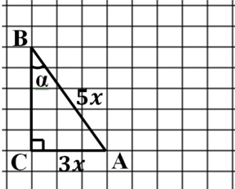
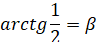 , тогда
, тогда  . Построим прямоугольный треугольник с углом β, так чтобы
. Построим прямоугольный треугольник с углом β, так чтобы 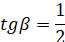 , т.е. противолежащий катет и прилежащий должны быть пропорциональны числам 1 и 2 (∠ADM=β). При этом один из катетов лежит на продолжении катета AC
, т.е. противолежащий катет и прилежащий должны быть пропорциональны числам 1 и 2 (∠ADM=β). При этом один из катетов лежит на продолжении катета AC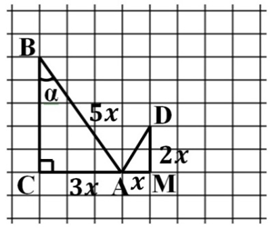
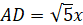 .
.
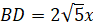 .
.

